Harmonijski red (matematika)

Šablon:Infinitezimalni račun U matematici, harmonijski red je beskonačni red

$\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots .$

Njegovo ime potiče iz koncepta harmonika, u muzici: talasne dužine harmonika vibrirajuće žice su 1/2, 1/3, 1/4, itd., osnovne talasne dužine. Svaki član reda nakon prvog je harmonijska sredina susjednih članova.

Divergencija harmonijskog reda

Harmonijski red divergira u beskonačnost, iako to radi prilično sporo (suma prvih 10⁴³ članova iznosi manje od 100). Jedan od načina da dokažemo ovu divergenciju je da uočimo da je harmonijski red član po član veći ili jednak drugom divergentnom redu:

$\begin{array}{cc}\sum _{k=1}^{\mathrm{\infty }}\frac{1}{k}& =1+\left[\frac{1}{2}\right]+[\frac{1}{3}+\frac{1}{4}]+[\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}]+[\frac{1}{9}+\cdots ]+\cdots \\ & >1+\left[\frac{1}{2}\right]+[\frac{1}{4}+\frac{1}{4}]+[\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}]+[\frac{1}{16}+\cdots ]+\cdots \\ & =1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots .\end{array}$

Suma beskonačno mnogo Šablon:Razlomak očito divergira u beskonačnost, što znači da i harmonijski red divergira. Preciznije, ako je $s_{2^k}$ 2^k-ta parcijalna suma harmonijskog reda, tada je

$s_{2^k}\ge 1+\frac{k}{2},$

što očito divergira, ali sporo (po logaritamskom pravilu). Ovaj dokaz, zahvaljujući Nicoleu Oresmeu, je vrhunac srednjovijekovne matematike. Ovo je još uvijek standardni dokaz koji se i danas obrađuje na časovima matematike .

Drugi dokaz koristi Cauchyjev integralni test konvergencije, koji poredi harmonisjki red sa (divergentnim) integralom Šablon:Razlomak u granicama od 1 do beskonačnosti.

Čak i suma recipročnih prostih brojeva divergira u beskonačnost, iako to čini sporije; poznati dokazi ove činjenice su mnogo teži.

Konvergencija alternativnog harmonijskog reda

Prvih četrnaest parcijalnih suma alternativnog harmonijskog reda (segmenti srnih linija) prikazani kako konvergiraju prema prirodnom logaritmu od 2 (crvena linija).

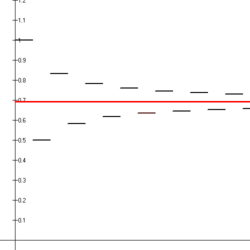
Alternativni harmonijski red konvergira:

$\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k+1}}{k}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots =\ln 2=0.6931471806\dots .$

Ova jednakost posljedica je Mercatorovog reda, Taylorovog reda za prirodni logaritam. Druga jednakost, slična po formi Mercatorovom redu, je:

$\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{2k+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\arctan (1)=\frac{\pi }{4}.$

Ovo je posljedica predstavljanja Taylorovog reda funkcije tangensa (koja ima radijus konvergencije 1).

Parcijalne sume

ntta parcijalna suma divergentnog harmonijskog reda,

$H_n=\sum _{k=1}^n\frac{1}{k},$

naziva se n-ti harmonijski broj.

Razlika između n-tog harmonijskog borja i prirodnog logaritma od n konvergira u vrijednost Euler-Mascheroniove konstante.

Razlika između različitih harmonijskih brojava nikada nije cijeli broj.

Jeffrey Lagarias je, 2001. godine, dokazao da je Riemannova hipoteza logički jednaka iskazu

$\sigma (n)\le H_n+\ln (H_n)e^{H_n}\text{ za svako }n\in \mathbb{N},$

gdje σ(n) označava pozitivne djelioce broja n.

Opći harmonijski red

Opći harmonijski red je red u obliku

$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{an+b}.$

Svi opći harmonijski redovi divergiraju.

p-red

p-red je red oblika

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^p},$

za svaki pozitivan realan broj p. Red je uvijek konvergentan ako je p > 1 (u tom slučaju naziva se hiperharmonijski red), dok je divergentan u ostalim slučajevima. Za slučaj p = 1, red postaje harmonijski red. Ako je p > 1 tada je suma red ζ(p), npr., Riemannova zeta-funkcija izračunata u p.

Slučajni harmonijski red

Byron Schmuland sa Univerziteta u Alberti ispitao je osobine slučajnog harmonijskog reda

$\sum _{n=1}^{\mathrm{\infty }}\frac{s_n}{n},$

gdje su s_n nezavisne, identično raspoređene slučajne promjenljive koje imaju vrijednost +1 i −1, sa jednakom vjerovatnoćom od Šablon:Razlomak. Pokazao je da ova suma konvergira sa vjerovatnoćom 1, te da je konvergentna slučajna promjeljiva sa nekim interesantnim osobinama. Na primjer, funkcija gustine ove slučajne varijable je izračunata da na +2 ili na −2 ima vrijednost 0,124 999 999 999 999 999 999 999 999 999 999 999 999 999 7642 ..., razlikujući se od Šablon:Razlomak za manje od 10⁻⁴². Schmulandov rad objašnjava zašto je ova vjerovatnoća blizu, ali ne iznosi tačno Šablon:Razlomak.

"Iscrpljeni" harmonijski red

Šablon:Glavni Za "iscrpljeni" harmonijski red, gdje su svi članovi sa brojem 9 u nazivniku uklonjeni, može se pokazati da konvergira, te da je njegova vrijednost manja od 80. U stvari, kada se bilo koji član, koji sadrži neki niz brojeva, ukljoni, red opet konvergira.

Također pogledajte

• Kompleksni logaritam
• Harmonijski brojnumber
• Riemannova zeta-funkcija
• Mnogo dokaza divergencije harmonijskih redova : "The Harmonic Series Diverges Again and Again", The AMATYC Review, 27 (2006), str. 31-43.