Torus

Torus je obrtna površ koja se dobija kada se rotira kružnica u trodimenzionom prostoru oko ose komplanarne sa kružnicom, a koja ne dodiruje krug.

Torus

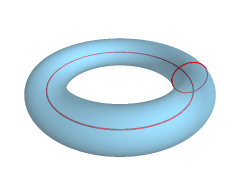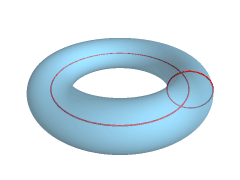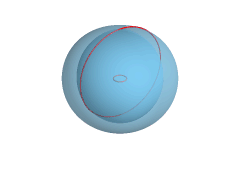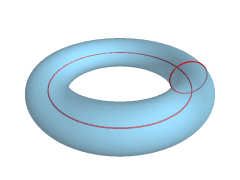
1. Ako osa rotacije ne dodiruje kružnicu površ ima oblik prstena i naziva se prstenasti torus ili samo torus.
2. U slučaju da je osa rotacije tangenta kružnice dobijena površ se naziva rog torus
3. kada za osu rotacije uzmemo tetivu kružnice rezultujuća površ je vretenasti torus.

Jednačina

Kao takva površ torus ima "rupu". Ako označimo sa c radijus od centra "rupe" do centra torusa, a sa a radijus torusa dolazimo do njegove parametarske jednačine:

$\{\begin{array}{c}x=(c+acosv)cosu\\ y=(c+acosv)sinu\\ z=asinv\end{array}$ za $u,v\in [0,2\pi )$

gdje su $u$ i $v$ uglovi koji čine puni krug, tako da njihove vrijednosti počinju i završavaju u istoj tački

$c$ je udaljenost od centra cijevi do središta torusa, $a$ je promjer cijevi. $c$ je glavni radijus, a $a$ sporedni radijus.

Implicitna jednačina u Kartezijevim koordinatama je

${(c-\sqrt{x^2+y^2})}^2+z^2=a^2,$

Površina i zapremina

Površina torusa je

$P=\left(2\pi r\right)\left(2\pi R\right)=4{\pi }^{2}ca$

a zapremina

$V=\left(\pi a^2\right)\left(2\pi c\right)=2{\pi }^{2}c{a}^2$

$V=2{\pi }^{2}R{r}^2,$

Dokaz

$S=S_1-S_2,$

$S_1=\pi (R+a{)}^2,$

$S_2=\pi (R-a{)}^2$

Prema Pitagorinoj teoremi imamo

$a=\sqrt{r^2-z^2}$

$S_1=\pi (R+\sqrt{r^2-z^2}{)}^2$
$S_2=\pi (R-\sqrt{r^2-z^2}{)}^2$

$S=\pi (R+\sqrt{r^2-z^2}{)}^2-\pi (R-\sqrt{r^2-z^2}{)}^2$

$S=\pi [(R+\sqrt{r^2-z^2}{)}^2-(R-\sqrt{r^2-z^2}{)}^2]$

$S=\pi (R^2+2R\sqrt{r^2-z^2}+r^2-z^2-R^2+2R\sqrt{r^2-z^2}-r^2+z^2)$

$S=\pi (2R\sqrt{r^2-z^2}+2R\sqrt{r^2-z^2})$

$S=4\pi R\sqrt{r^2-z^2}$

$V=\underset{-r}{\overset{r}{\int }}S(z)dz$

$V=\underset{-r}{\overset{r}{\int }}4\pi R\sqrt{r^2-z^2}dz$

$V=4\pi R\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz$

$\frac{du}{dz}=\frac{d\sqrt{r^2-z^2}}{dz}$

$\frac{d\sqrt{r^2-z^2}}{dz}\frac{d(r^2-z^2)}{d(r^2-z^2)}$

$\frac{d\sqrt{r^2-z^2}}{d(r^2-z^2)}\frac{d(r^2-z^2)}{dz}$

$\frac{du}{dz}=\frac{1}{2(r^2-z^2)}(\frac{d{r}^2}{d{z}^2}-\frac{d{z}^2}{dz})=\frac{1}{2(r^2-z^2)}(0-2z)=\frac{-2z}{2(r^2-z^2)}=-\frac{z}{(r^2-z^2)}$

$du=-\frac{z}{r^2-z^2}dz$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=z\sqrt{r^2-z^2}{|}_{-r}^r-\underset{-r}{\overset{r}{\int }}-\frac{z^2}{\sqrt{r^2-z^2}}dz$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=z\sqrt{r^2-z^2}{|}_{-r}^r-\underset{-r}{\overset{r}{\int }}\frac{-z^2-r^2+r^2}{\sqrt{r^2-z^2}}dz$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=z\sqrt{r^2-z^2}{|}_{-r}^r-\underset{-r}{\overset{r}{\int }}\frac{r^2-z^2}{\sqrt{r^2-z^2}}dz+\underset{-r}{\overset{r}{\int }}\frac{r^2}{\sqrt{r^2-z^2}}dz$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=z\sqrt{r^2-z^2}{|}_{-r}^r-\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz+r^2\underset{-r}{\overset{r}{\int }}\frac{1}{\sqrt{r^2-z^2}}dz$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz+\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=z\sqrt{r^2-z^2}{|}_{-r}^r+r^2\underset{-r}{\overset{r}{\int }}\frac{1}{\sqrt{r^2(1-\frac{z^2}{r^2})}}dz$

$2\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=z\sqrt{r^2-z^2}{|}_{-r}^r+r^2\underset{-r}{\overset{r}{\int }}\frac{1}{\sqrt{(1-(\frac{z}{r}{)}^2)}}d(\frac{z}{r})$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=\frac{z\sqrt{r^2-z^2}+r^2\arcsin (\frac{z}{r})}{2}{|}_{-r}^r$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=\frac{r\sqrt{r^2-r^2}+r^2\arcsin (\frac{r}{r})}{2}-\frac{-r\sqrt{r^2-(-r{)}^2}+r^2\arcsin (\frac{(-r)}{r})}{2}$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=\frac{r^2\arcsin (1)-r^2\arcsin (-1)}{2}$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=\frac{r^2}{2}(\frac{\pi }{2}-(-\frac{\pi }{2}))$

$\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz=\frac{r^2\pi }{2}$

$V=4\pi R\underset{-r}{\overset{r}{\int }}\sqrt{r^2-z^2}dz\to V=4\pi R\frac{r^2\pi }{2}$

$V=2{\pi }^{2}R{r}^2,$

Prstenasti torus

• 

Parametarska jednačina prstenastog torusa je

$\{\begin{array}{c}x=(c+acosv)cosu\\ y=(c+acosv)sinu\\ z=asinv\end{array}$

za $u,v\in [0,2\pi )$ $ia>c$

Koficienti prve kvadratne forme su

$E=(c+acosv{)}^2$

$F=0$

$G=a^2$

dok za koeficiente druge kvadratne forme dobijamo

$L=-(c+acosv)cosv$

$M=0$

$N=-a$

Gausova i srednja kriva su date sa:

$K_G=\frac{cosv}{a(c+acosv)}$

$K_S=\frac{-c+2acosv}{2a(c+acosv)}$

Rog torus

• 

Uzimajući u jednačini

$\{\begin{array}{c}x=(c+acosv)cosu\\ y=(c+acosv)sinu\\ z=asinv\end{array}$

da je $c=a$ dobijamo parametarsku jednačinu rog torusa

$\{\begin{array}{c}x=a(1+cosv)cosu\\ y=a(1+cosv)sinu\\ z=asinv\end{array}$

Za koeficiente prve kvadratne forme dobijamo:

$E=4a^{2}co{s}^4(\frac{1}{2}v)$

$F=0$

$G=a^2$

dok su koeficienti druge kvadratne forme rog torusa:

$L=-2aco{s}^2(\frac{1}{2})cosv$

$M=0$

$N=-a$

Vretenasti torus

• 

Kod vretenastog torusa parametarska jednačina, formule za koeficiente prve i druge kvadratne forme i formule za izračunavanje srednje i Gausove krive su iste kao i kod prstenastog torusa, uz uslov $c<a$.

Izvori

Rotacione površi i njihova vizuelizacija u programskom paketu Mathematica Niš, novembar 2013.Šablon:Mrtav link Šablon:Commons